Algebra 1 Chapter 2 Review 1 Evaluate Each Using the Values Given

2.3: Evaluate, Simplify, and Translate Expressions (Part ane)

Last updated
Salve as PDF

Page ID: 4978

Skills to Develop

Evaluate algebraic expressions
Identify terms, coefficients, and similar terms
Simplify expressions by combining like terms
Translate word phrases to algebraic expressions

Be prepared!

Before you lot go started, have this readiness quiz.

Is $n ÷ five$ an expression or an equation? If you missed this problem, review Example ii.one.4.
Simplify $4^5$. If you lot missed this problem, review Example 2.i.6.
Simplify $one + 8 • 9$. If yous missed this problem, review Instance two.ane.eight.

Evaluate Algebraic Expressions

In the concluding department, we simplified expressions using the order of operations. In this section, we'll evaluate expressions—again following the lodge of operations.

To evaluate an algebraic expression means to notice the value of the expression when the variable is replaced by a given number. To evaluate an expression, nosotros substitute the given number for the variable in the expression and and so simplify the expression using the guild of operations.

Example $\PageIndex{i}$: evaluate

Evaluate $x + 7$ when

$x = 3$
$x = 12$

Solution

To evaluate, substitute $iii$ for $x$ in the expression, and then simplify.

	$x + seven$
Substitute.	$\textcolor{cherry}{3} + 7$
Add.	$10$

When $ten = 3$, the expression $x + 7$ has a value of $ten$.

To evaluate, substitute $12$ for $x$ in the expression, and then simplify.

	$x + 7$
Substitute.	$\textcolor{cherry-red}{12} + 7$
Add together.	$xix$

When $ten = 12$, the expression $10 + 7$ has a value of $xix$. Discover that nosotros got different results for parts (a) and (b) even though nosotros started with the same expression. This is considering the values used for $10$ were different. When we evaluate an expression, the value varies depending on the value used for the variable.

do $\PageIndex{1}$

Evaluate: $y + 4$ when

$y = vi$
$y = 15$

Answer a: $10$
Reply b: $nineteen$

practise $\PageIndex{two}$

Evaluate: $a − v$ when

$a = 9$
$a = 17$

Respond a: $4$
Answer b: $12$

Example $\PageIndex{ii}$

Evaluate $9x − two$, when

$x = five$
$x = 1$

Solution

Think $ab$ means $a$ times $b$, so $9x$ ways $9$ times $x$.

To evaluate the expression when $x = 5$, we substitute $five$ for $x$, and and so simplify.

	$9x - 2$
Substitute $\textcolor{red}{5}$ for x.	$9 \cdot \textcolor{scarlet}{5} - 2$
Multiply.	$45 - ii$
Subtract.	$43$

To evaluate the expression when $10 = 1$, we substitute $ane$ for $x$, and then simplify.

	$9x - ii$
Substitute $\textcolor{red}{ane}$ for x.	$9 \cdot \textcolor{crimson}{1} - 2$
Multiply.	$nine - ii$
Subtract.	$7$

Notice that in office (a) that nosotros wrote $nine • 5$ and in function (b) we wrote $9(1)$. Both the dot and the parentheses tell u.s. to multiply.

exercise $\PageIndex{iii}$

Evaluate: $8x − iii$, when

$x = 2$
$x = 1$

Reply a: $xiii$
Answer b: $v$

practise $\PageIndex{iv}$

Evaluate: $4y − 4$, when

$y = three$
$y = five$

Answer a: $8$
Respond b: $xvi$

Example $\PageIndex{iii}$: evaluate

Evaluate $x^two$ when $ten = x$.

Solution

We substitute $10$ for $x$, and then simplify the expression.

	$ten^{2}$
Substitute $\textcolor{red}{10}$ for ten.	$\textcolor{scarlet}{10}^{2}$
Use the definition of exponent.	$ten \cdot 10$
Multiply	$100$

When $x = 10$, the expression $x^2$has a value of $100$.

exercise $\PageIndex{five}$

Evaluate: $10^two$ when $ten = 8$.

Answer: $64$

exercise $\PageIndex{6}$

Evaluate: $10^3$when $10 = vi$.

Answer: $216$

Example $\PageIndex{four}$: evaluate

Evaluate $2^x$ when $ten = 5$.

Solution

In this expression, the variable is an exponent.

	$2^{x}$
Substitute $\textcolor{cherry}{five}$ for ten.	$2^{\textcolor{red}{five}}$
Use the definition of exponent.	$ii \cdot 2 \cdot 2 \cdot 2 \cdot ii$
Multiply	$32$

When $x = 5$, the expression $2^x$ has a value of $32$.

exercise $\PageIndex{7}$

Evaluate: $2^ten$ when $x = half-dozen$.

Answer: $64$

exercise $\PageIndex{8}$

Evaluate: $3^x$ when $x = 4$.

Answer: $81$

Example $\PageIndex{five}$: evaluate

Evaluate $3x + 4y − 6$ when $x = x$ and $y = 2$.

Solution

This expression contains ii variables, and then we must make 2 substitutions.

	$3x + 4y − 6$
Substitute $\textcolor{red}{x}$ for 10 and $\textcolor{blue}{ii}$ for y.	$3(\textcolor{cherry-red}{10}) + iv(\textcolor{bluish}{2}) − 6$
Multiply.	$xxx + eight - 6$
Add and subtract left to right.	$32$

When $x = 10$ and $y = two$, the expression $3x + 4y − 6$ has a value of $32$.

practice $\PageIndex{ix}$

Evaluate: $2x + 5y − four$ when $x = xi$ and $y = 3$

Answer: $33$

do $\PageIndex{10}$

Evaluate: $5x − 2y − 9$ when $x = vii$ and $y = eight$

Answer: $x$

Instance $\PageIndex{6}$: evaluate

Evaluate $2x^2 + 3x + 8$ when $ten = 4$.

Solution

We need to be careful when an expression has a variable with an exponent. In this expression, $2x^2$ means $two • ten • x$ and is different from the expression $(2x)^ii$, which means $2x • 2x$.

	$2x^{2} + 3x + 8$
Substitute $\textcolor{red}{four}$ for each x.	$two(\textcolor{cherry-red}{iv})^{2} + 3(\textcolor{blood-red}{4}) + 8$
Simplify iv².	$2(16) + 3(4) + eight$
Multiply.	$32 + 12 + eight$
Add together.	$52$

practise $\PageIndex{11}$

Evaluate: $3x^2 + 4x + 1$ when $x = 3$.

Answer: $40$

practise $\PageIndex{12}$

Evaluate: $6x^ii − 4x − vii$ when $x = 2$.

Answer: $9$

Identify Terms, Coefficients, and Like Terms

Algebraic expressions are made upwardly of terms. A term is a constant or the production of a constant and one or more variables. Some examples of terms are $7$, $y$, $5x^two$, $9a$, and $13xy$.

The constant that multiplies the variable(due south) in a term is chosen the coefficient. We tin can think of the coefficient equally the number in forepart of the variable. The coefficient of the term $3x$ is $3$. When we write $ten$, the coefficient is $1$, since $ten = 1 • 10$. Table $\PageIndex{1}$ gives the coefficients for each of the terms in the left cavalcade.

Table $\PageIndex{i}$
Term	Coefficient
7	7
9a	9
y	1
5x^two	5

An algebraic expression may consist of i or more terms added or subtracted. In this chapter, nosotros will simply piece of work with terms that are added together. Table $\PageIndex{2}$ gives some examples of algebraic expressions with various numbers of terms. Observe that we include the operation earlier a term with information technology.

Table $\PageIndex{2}$
Expression	Terms
vii	7
y	y
x + 7	x, vii
2x + 7y + 4	2x, 7y, 4
3x²+ 4x² + 5y + 3	3x^ii, 4x², 5y, three

Instance $\PageIndex{7}$:

Identify each term in the expression $9b + 15x^two + a + 6$. Then identify the coefficient of each term.

Solution

The expression has 4 terms. They are $9b$, $15x^two$, $a$, and $6$.

The coefficient of $9b$ is $9$.

The coefficient of $15x^two$ is $xv$.

Remember that if no number is written earlier a variable, the coefficient is $1$. So the coefficient of a is $1$.

The coefficient of a constant is the abiding, and then the coefficient of $6$ is $6$.

exercise $\PageIndex{13}$

Identify all terms in the given expression, and their coefficients: $4x + 3b + 2$

Reply: The terms are $4x, 3b,$ and $2$. The coefficients are $iv, iii,$ and $2$.

exercise $\PageIndex{14}$

Identify all terms in the given expression, and their coefficients: $9a + 13a^2 + a^3$

Respond: The terms are $9a, 13a^two,$ and $a^3$, The coefficients are $nine, 13,$ and $i$.

Some terms share common traits. Look at the following terms. Which ones seem to take traits in mutual?

$5x, 7, due north^{2}, 4, 3x, 9n^{ii}$

Which of these terms are like terms?

The terms $7$ and $4$ are both constant terms.
The terms $5x$ and $3x$ are both terms with $x$.
The terms $n^two$ and $9n^2$ both have $north^2$.

Terms are called like terms if they have the same variables and exponents. All constant terms are besides like terms. And so among the terms $5x, 7, north^ii, 4, 3x, 9n^2, vii$ and $four$ are like terms, $5x$ and $3x$ are similar terms, and $due north^two$ and $9n^ii$ are like terms.

Definition: Like terms

Terms that are either constants or accept the same variables with the same exponents are like terms.

Case $\PageIndex{eight}$: identify

Identify the like terms:

$y^iii, 7x^ii, xiv, 23, 4y^iii, 9x, 5x^2$
$4x^two + 2x + 5x^2 + 6x + 40x + 8xy$

Solution

$y^iii, 7x^2, fourteen, 23, 4y^3, 9x, 5x^2$

Look at the variables and exponents. The expression contains $y^3, ten^two, 10$, and constants. The terms $y^three$ and $4y^3$ are like terms because they both have $y^3$. The terms $7x^2$ and $5x^2$ are like terms because they both have $x^two$. The terms $14$ and $23$ are similar terms because they are both constants. The term $9x$ does not have any similar terms in this list since no other terms have the variable $ten$ raised to the power of $1$.

$4x^2 + 2x + 5x^2 + 6x + 40x + 8xy$

Look at the variables and exponents. The expression contains the terms $4x^2, 2x, 5x^2, 6x, 40x$, and $8xy$ The terms $4x^2$ and $5x^2$ are similar terms because they both take $x^ii$. The terms $2x, 6x$, and $40x$ are like terms because they all accept $x$. The term $8xy$ has no like terms in the given expression considering no other terms contain the two variables $xy$.

exercise $\PageIndex{15}$

Identify the like terms in the list or the expression: $9, 2x^3, y^2, 8x^three, xv, 9y, 11y^2$

Answer: $9, 15$; $2x^three$ and $8x^3$, $y^ii$, and $11y^2$

exercise $\PageIndex{16}$

Place the like terms in the list or the expression: $4x^3 + 8x^2 + 19 + 3x^2 + 24 + 6x^3$

Reply: $4x^3$ and $6x^three$; $8x^2$ and $3x^2$; $19$ and $24$

Simplify Expressions by Combining Similar Terms

We can simplify an expression past combining the similar terms. What do you think $3x + 6x$ would simplify to? If you thought $9x$, you would be right!

We can see why this works by writing both terms as addition issues.

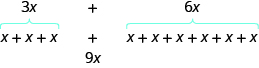
$CNX_BMath_Figure_02_02_001_img.jpg$

Add the coefficients and go on the same variable. Information technology doesn't matter what $10$ is. If you lot accept $3$ of something and add $6$ more of the same thing, the result is $9$ of them. For example, $iii$ oranges plus $6$ oranges is $ix$ oranges. We will talk over the mathematical properties behind this later.

The expression $3x + 6x$ has only 2 terms. When an expression contains more terms, information technology may be helpful to rearrange the terms so that like terms are together. The Commutative Belongings of Addition says that we tin can change the order of addends without changing the sum. Then nosotros could rearrange the following expression earlier combining like terms.

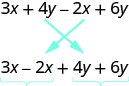
$CNX_BMath_Figure_02_02_015_img.jpg$

At present it is easier to see the like terms to exist combined.

HOW TO: COMBINE Like TERMS

Stride ane. Place like terms.

Step 2. Rearrange the expression so like terms are together.

Step 3. Add the coefficients of the like terms.

Case $\PageIndex{9}$: simplify

Simplify the expression: $3x + 7 + 4x + v$.

Solution

	$3x + 7 + 4x + 5$
Identify the like terms	$\textcolor{carmine}{3x} + \textcolor{blue}{7} + \textcolor{red}{4x} + \textcolor{blue}{5}$
Rearrange the expression, so the like terms are together.	$\textcolor{ruby-red}{3x} + \textcolor{blood-red}{4x} + \textcolor{blue}{7} + \textcolor{blue}{5}$
Add together the coefficients of the like terms.	$\textcolor{ruby-red}{7x} + \textcolor{blueish}{12}$
The original expression is simplified to...	$7x + 12$

exercise $\PageIndex{17}$

Simplify: $7x + 9 + 9x + 8$

Answer: $16x+17$

exercise $\PageIndex{xviii}$

Simplify: $5y + two + 8y + 4y + 5$

Answer: $17y+7$

Example $\PageIndex{10}$: simplify

Simplify the expression: $7x^2 + 8x + ten^two + 4x$.

Solution

	$7x^{2} + 8x + x^{2} + 4x$
Identify the like terms.	$\textcolor{red}{7x^{2}} + \textcolor{blue}{8x} + \textcolor{red}{ten^{2}} + \textcolor{blue}{4x}$
Rearrange the expression so like terms are together.	$\textcolor{blood-red}{7x^{ii}} + \textcolor{ruby-red}{ten^{2}} + \textcolor{blue}{8x} + \textcolor{bluish}{4x}$
Add the coefficients of the like terms.	$\textcolor{red}{8x^{ii}} + \textcolor{blueish}{12x}$

These are not like terms and cannot be combined. So $8x^two + 12x$ is in simplest form.

exercise $\PageIndex{19}$

Simplify: $3x^2 + 9x + x^ii + 5x$

Answer: $4x^2+14x$

exercise $\PageIndex{twenty}$

Simplify: $11y^ii + 8y + y^2 + 7y$

Answer: $12y^ii+15y$

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced past OpenStax and is licensed under a Artistic Eatables Attribution License 4.0 license.

schaefernouse1990.blogspot.com

Source: https://math.libretexts.org/Bookshelves/PreAlgebra/Book:_Prealgebra_%28OpenStax%29/02:_Introduction_to_the_Language_of_Algebra/2.03:_Evaluate_Simplify_and_Translate_Expressions_%28Part_1%29

	\(x + seven\)
Substitute.	\(\textcolor{cherry}{3} + 7\)
Add.	\(10\)

	\(x + 7\)
Substitute.	\(\textcolor{cherry-red}{12} + 7\)
Add together.	\(xix\)

	\(9x - 2\)
Substitute \(\textcolor{red}{5}\) for x.	\(9 \cdot \textcolor{scarlet}{5} - 2\)
Multiply.	\(45 - ii\)
Subtract.	\(43\)

	\(9x - ii\)
Substitute \(\textcolor{red}{ane}\) for x.	\(9 \cdot \textcolor{crimson}{1} - 2\)
Multiply.	\(nine - ii\)
Subtract.	\(7\)

	\(ten^{2}\)
Substitute \(\textcolor{red}{10}\) for ten.	\(\textcolor{scarlet}{10}^{2}\)
Use the definition of exponent.	\(ten \cdot 10\)
Multiply	\(100\)

Algebra 1 Chapter 2 Review 1 Evaluate Each Using the Values Given

2.3: Evaluate, Simplify, and Translate Expressions (Part ane)

Evaluate Algebraic Expressions

Identify Terms, Coefficients, and Like Terms

Simplify Expressions by Combining Similar Terms

Contributors and Attributions

0 Response to "Algebra 1 Chapter 2 Review 1 Evaluate Each Using the Values Given"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel

	\(2^{x}\)
Substitute \(\textcolor{cherry}{five}\) for ten.	\(2^{\textcolor{red}{five}}\)
Use the definition of exponent.	\(ii \cdot 2 \cdot 2 \cdot 2 \cdot ii\)
Multiply	\(32\)

	\(3x + 4y − 6\)
Substitute \(\textcolor{red}{x}\) for 10 and \(\textcolor{blue}{ii}\) for y.	\(3(\textcolor{cherry-red}{10}) + iv(\textcolor{bluish}{2}) − 6\)
Multiply.	\(xxx + eight - 6\)
Add and subtract left to right.	\(32\)

	\(2x^{2} + 3x + 8\)
Substitute \(\textcolor{red}{four}\) for each x.	\(two(\textcolor{cherry-red}{iv})^{2} + 3(\textcolor{blood-red}{4}) + 8\)
Simplify iv².	\(2(16) + 3(4) + eight\)
Multiply.	\(32 + 12 + eight\)
Add together.	\(52\)

	\(3x + 7 + 4x + 5\)
Identify the like terms	\(\textcolor{carmine}{3x} + \textcolor{blue}{7} + \textcolor{red}{4x} + \textcolor{blue}{5}\)
Rearrange the expression, so the like terms are together.	\(\textcolor{ruby-red}{3x} + \textcolor{blood-red}{4x} + \textcolor{blue}{7} + \textcolor{blue}{5}\)
Add together the coefficients of the like terms.	\(\textcolor{ruby-red}{7x} + \textcolor{blueish}{12}\)
The original expression is simplified to...	\(7x + 12\)

	\(7x^{2} + 8x + x^{2} + 4x\)
Identify the like terms.	\(\textcolor{red}{7x^{2}} + \textcolor{blue}{8x} + \textcolor{red}{ten^{2}} + \textcolor{blue}{4x}\)
Rearrange the expression so like terms are together.	\(\textcolor{blood-red}{7x^{ii}} + \textcolor{ruby-red}{ten^{2}} + \textcolor{blue}{8x} + \textcolor{bluish}{4x}\)
Add the coefficients of the like terms.	\(\textcolor{red}{8x^{ii}} + \textcolor{blueish}{12x}\)